![]()
Article Type: Short Communication
Sample Size Calculation in Various Medical Research
Year: 2024; Volume: 4; Issue: 3; Page No: 22–29
![]() https://doi.org/10.55349/ijmsnr.2024432229
https://doi.org/10.55349/ijmsnr.2024432229
Affiliations: Assistant Professor in Statistics (Biostatistics), Department of Community Medicine, Sri Venkateshwaraa Medical College Hospital & Research Centre, Ariyur, Pondicherry – 605 102. Email ID: senthilvel99@gmail.com
| How to cite this article: Vasudevan S. Sample Size Calculation in Various Medical Research. Int J Med Sci and Nurs Res 2024;4(3):22–29. DOI: https://doi.org/10.55349/ijmsnr.2024432229 |
Corresponding Author:
Dr. Senthilvel Vasudevan, Ph.D,
Assistant Professor in Statistics (Biostatistics),
Department of Community Medicine,
Sri Venkateshwaraa Medical College Hospital & Research Centre,
Ariyur, Pondicherry – 605 102. India.
Email ID: senthilvel99@gmail.com
ORCID: https://orcid.org/0000-0001-7175-3534
Article Summary: Submitted: 15-July-2024; Revised: 28-August-2024; Accepted: 23-September-2024; Published: 30-September-2024
Abstract
Background: Sample size is the backbone of a scientific study/research in any field of science. It is mandatory at time of preparing proposal for a particular study. Large sample size is not needed and it is unethical also. Similarly, very too smaller sample is also.
Materials and Methods: The adequate sample would be calculated either manually by using some formulae or using some existing statistical software like Statistical Package for Social Sciences (SPSS), Epi Info or online software with some conditions related to that study/research.
Results: Previously existing literatures are not available then; sample size is to be determined based on pilot study in that region. In this article discuss about the sample size, its calculations, determine sample size we have to follow the conditions, knowledge to be needed at the time of calculating sample size, how much statistical power fix to a study, sample size and ethics, type-I and type-II errors, interpreting results of larger and smaller samples.
Conclusion: From this article, I have concluded that a researcher has to write the proposal for his/her studies, find the appropriate parent/key article, finding the risk factors related to your studies, and the final step is to find the sample size with the help of a statistical expert. Then only proceed the study by the researchers.
Keywords: sample size, proposal, statistical power, hypotheses, type-I and type-II errors, medical research
Full Text
Introduction
One of the most important aspects of planning in medical, clinical, epidemiology, or translational study is the calculation of sample size. In medical research sample size is an essential tool for all types of studies. [1] It is naturally feasible to study the whole population in any type of studies in medical research. All studies are usually conducted based on sample size with some inclusion and exclusion criteria. [2] Sample size is playing an important role in the analysis part and as well as in the results writing. [3] Why because, the conclusions are drawing from the analysis of sample size determined for a study and which is to be generalized to the whole/entire population of a part/region/state/country. This is only following by the National Sampling Survey and all Government organizations. Most of the Government related sample survey was very much useful in the policy making process/in decision taking in the nationwide. [4] The sample size should be adequate/enough in size then, the researcher can start or do the study. This is very important and mandatory also. Sample size is calculating by using manually by some established and appropriate formulae which is already exists in the literatures or documents. [5]
Materials and Methods:
Calculation of Sample Size: [6]
Sample size is the subset of a study population. Sample size to calculate to show that under some conditions as per your inclusion and exclusion criteria. To fix an adequate sample size mainly to minimize money, man power, time to conduct the study, and to show at the time of proposal presentation of the sample size calculation to the Scientific Research Committee (SRC) and Institutional Ethical Committee (IEC) and for the funding agency that the study has had a reasonable chance to obtain a correct result. In statistics, sample size is the measure of the number of individual samples ad that shall be used in a study/experiment. Estimation of sample Size by the following three ways: (a). Formulae by manual calculations; (b). Sample size tables; (c). Software like Epi Info [7], nMaster 2.0 [8], OpenEpi 3.01 version [9] and online sample size calculator. Hence, by some conditions (inclusion and exclusion criteria) a set of participants will be selected from the population, which is less in number/size but adequately enough sample size represents the population from which it is drawn so that true inferences about the population can be made from the obtained results. This set of patients/individuals is known as “Sample or Sample Size” as show in Figure – 1
Figure – 1 Showing population and selection of a sample

Sample Size, Ethical Considerations and its effects to the participants
Sample size calculation is an essential procedure/process and mandatory in all the studies. If sample size is very high in a study, then the sampling error will reduce and get the accurate results for a particular study. Then, results will be the better representative of the study population. After certain points, adding more samples isn’t giving that much effect in the accuracy of the study. So, put the effort and expense to those recruited patients isn’t worth to a researcher. Furthermore, it will give trouble to the extra patients in the study. This is unethical. In another way also unethical things will happen. For example, suppose a researcher have taken smaller sample size than the calculated sample size ie. Excess patients to be included in their study. In this situation, those patients’ have to face physical and psychological disturbance at the time of face-face interviews, their physical check-up, blood sampling, routine check-up ad other procedures. These thigs to be avoided when the researcher conducted their research/study within the calculated sample size.
Statistical Power [10 – 12]
Statistical power means the ability of a study/experimental design and hypothesis setup to detect a particular effect if it is truly present. In any medical research or any research, the statistical power always at least 80% and above only as show in Table–1. A researcher should know in what way to increase the statistical power of their study. In the following ways: Increase the potential effect of size by manipulating independent variable more strongly to the study, increase sample size to that study, increase the level of significance (α) and to reduce measurement error by increasing the precision and accuracy of your measurement equipment and test procedures of the study.
Table – 1 Showing β and Z constant value by conversion according the power of the study
| Power |
80% |
85% | 90% |
95% |
| Value |
0.8416 |
1.0364 | 1.2816 |
1.6449 |
Conditions follows at the time of determining the sample size for a study: [12]
At the time of sample size calculation, a researcher has to remember the following conditions.
- What is the primary objective of the study?
- Whether the researcher choose an appropriate key article/parent article to his/her research topic?
- Is the parent/key article co-inside up to 50% or 60% or maximum 80% to their primary objective or not?
- What is the main outcome measure of the study? Whether it is a continuous or categorical outcome?
- How will the data be analyzed to detect a group difference ad mentioned in the statistical analysis part?
- How small a difference is clinically important to detect?
- How much variability is in our study population/group?
- What is the desired level of significance (α) and Type II error (b)?
- What is the anticipated/expected drop-out percentage and non-response percentage?
Type I, Type II, and Level of Significant
This type of knowledge one can gets from previous published or existing studies/articles, and as well as from some pilot studies. If information is lacking about the proposed study, then there is no good way to calculate the sample size.
Type-I error means rejecting H0 when H0 is true, Type-II error means failing to reject H0 when H0 is false, level of significant (α) means type-I error rate, β denotes type-II error rate and statistical power (1–β) means probability of detecting group difference given the size of the effect (D) and the sample size of the trial (N) as shown in Table–2 and Table–3.
Table – 2 Showing disease status and test results
| Test Results |
Disease Status |
|
|
Present |
Absent |
|
| Positive |
True Positive (Sensitivity) |
False Positive |
| Negative |
False Negative |
True Negative (Specificity) |
Table – 3 Showing Type – I error and Type – II error
| Test Results |
Significant Difference is |
|
|
Present (H0 not true) |
Absent (H0 is true) |
|
| Positive |
No error 1 – β |
Type I error α |
| Negative |
Type II error β |
No error 1 – α |
Here, α: significance level; 1-β: power
Adequate Precision in the process of calculation of Sample Size:
In descriptive study, summary statistics (mean, proportion), reliability (or) precision. By giving “Confidence Interval (CI)” wider the 95% C.I – sample statistic isn’t reliable and it may not give an accurate estimate of the true value of the population parameter.
Sample size formulae for various situations
When standard deviation value was known
n = Z α2 S2 /d2
Here, S = Standard Deviation
Example:
A study is to be conducted to determine the parameter Body Mass Index in a community. From a previous and recent published article, a Standard Deviation (σ) of 46 was taken. Allowable/ Sample error (d) was taken as 4 and level of confidence was 99%. How many subjects should be included in this study?
Zα/2 = 2.58, σ = 46, Allowable Error (d) = 4
n = Z α2 S2 /d2
n =
(2.58)2 x (46)2
———————-
42
n = 880.3 ~ 881 (Calculated minimum sample size)
When single proportion was given
n = Zα/2 2 *P* (1–P)/d2
Where, Zα = 1.96 for 95% confidence level
Zα = 2.58 for 99% confidence level
Example:
To determine/estimate proportion of anaemic among school going children. So, in the key article, the anaemic proportion was 30%. The researcher wants to compute the minimum sample size required to his/her study at 95% confidence level and allowable error up to 4% of the study population.
n = Zα/2 2 *P* (1–P)/d2
Zα/2 = 1.96; P = 30%; d = accuracy of estimate/allowable error = 4%
n =
(1.96)2 x 0.3 (1 – 0.3)
——————–
(0.4)2
n = 504.21 ~ 505 (Calculated minimum sample size)
Figure – 2 Distribution of three bits of information required to determine the sample size in clinical study

Researcher fixes probabilities of type I and II errors as shown in Figure – 2
Prob (type I error) = Prob (reject H0 when H0 is true) = α
Smaller error –> greater precision –> need more information –> need larger sample size
Prob (type II error) = Prob (Accept H0 when H0 is false) = β
Statistical Power = 1 – β
More power –> smaller error –> need larger sample size
Quantities related to the research question (defined by the researcher), size of the measure of interest to be detected, difference between two or more means, difference between two or more proportions, odds ratio, relative risk, correlation, regression coefficients, and change in R2, etc. The magnitude of these values depends on the research question and objective of the study (for example, clinical relevance).
Clinical Effect Size
Clinical effect size is a measure of (a). the amount of change in a sample of patients who undergo a treatment, (b). the amount of change in a sample of patients who undergo a treatment compared to a control group. It explains to the researcher how much difference in a treatment. It is truly an estimate and often the most challenging aspect of sample size planning only.
Large difference will be happened by small sample size fixation. Similarly small differences will be happened large sample size and it would be a cost-effective and benefited to the community.
Sample size formulae for comparing of two means:
n = 2 S2 (Zα+ Zβ)2 /d2
Where S = SD; d = difference
Zα = 1.96 for 95% confidence level; Zα = 2.58 for 99% confidence level
Zβ = 0.842 for 80% power; Zβ = 1.282 for 90% power
Sample size formulae for comparing of two proportions:
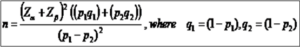
Here, Zα = 1.96 for 95% confidence level; Zα = 2.58 for 99% confidence level
Zβ= 0.842 for 80% power; Zβ= 1.282 for 90% power
Example:
For example, does the consumption of large doses of vitamin A in tablet form prevent breast cancer?
The data from the tumor-registry data that incidence rate of breast cancer over a 1-year period for women aged 45–49 years is 150 cases per 100,000 women randomized to Vitamin A vs. placebo
Test H0: p1 = p2 vs. HA : p1 < p2
Assume 2-sided test with a = 0.05 and 80% power
p1 = 150 per 100,000 = 0.0015
p2 = 120 per 100,000 = 0.0012 (20% rate reduction)
D = p1 – p2 = 0.0003
z1-α/2 = 1.96 z1-β = .84
n = 234,882 per group. This sample size is too large.
Sample Size Formula to Compare Two Means from Independent Samples
Null Hypothesis, H0: m1 = m2
In this, α level, β level (1 – power), Expected population difference (D= |m1 – m2|), and Expected population standard deviation (s1, s2)
Example:
Research question: Does a special diet help to reduce cholesterol levels?
Suppose a researcher wishes to determine sample size to detect a 10 mg/dl difference in cholesterol level in a diet intervention group compared to a control (no diet) group
Subjects with baseline total cholesterol of at least 300 mg/dl randomized.
Group 1: Six-week diet intervention
Group 2: No changes in diet
Investigator wants to compare total cholesterol at the end of the six-week study
Statistical Analysis: Two sample t-test. This test for comparison of two means for independent samples
H0: m1 = m2 vs. HA: m1 < m2
Sample size calculation for continuous outcome when two independent samples are given
Test H0: m1 = m2 vs. HA: m1 < m2
Two-sided alternative and assume outcome normally distributed with S = Standard Deviation; d=difference between two means.
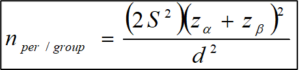
S= standard deviation; d=difference between two means; Zα = 1.96 for 95% confidence level; Zβ= 1.282 for 90% power
Examples:
Research Question: Does a special diet help to reduce cholesterol levels?
Test H0: m1=m2 vs. HA : m1 < m2
Assume 2-sided test with a=0.05 and 90% power
d = m1 – m2 = 10 mg/dl
s1= s2 = (50 mg/dl)
za = 1.96 zb = 1.28
Sample Size = n per group = 525
Suppose 10% loss to follow-up expected,
adjust n = 525 / 0.9
Calculated minimum sample size = 584 (per group)
Define research question well, consider study design, type of response variable, and type of data analysis, decide on the type of difference or change you want to detect (make sure it answers your research question), choose a, b and use appropriate equation for sample size calculation or sample size tables or software level;
Pragmatic approach to decision taking on sample size
A researcher has to remember the following steps:
- Researcher has to remember that there is no standard answer.
- Initiate early discussion among research team members.
- Use correct assumptions to consider various possibilities.
- Consider other factors like, availability of cases, cost, time.
- Make a balanced choice
- Ask if this number gives you a reasonable prospect of coming to useful conclusion.
- If yes, proceed. If not, reformulate your problem for the particular study.
Sample Size calculation and how to write the Sample Size calculation for the medical research?
Cross-Sectional Study
In cross-sectional studies to estimate the prevalence of unknown parameter(s) is the main objective of the study population using a random sampling method. Adequate sample size is needed to estimate the population prevalence with a good allowable error.
To calculate this adequate sample size would be used for calculating the adequate sample size for a prevalence study by the following simple formula.
? =
Z2 * P * (1-P)
—————–
d2
Here, n = sample size, Z = the statistic corresponding to level of confidence, P = expected prevalence (which can be obtained from previous existing similar type of studies (or) a pilot study conducted by the researchers, and d = precision (which is corresponding to effect size). Always, level of confidence aimed as 95%, most researchers express their results with 95% confidence interval. However, in clinical studies some researchers want to be more confident can chose a 99% confidence interval.
Choose a key/parent article which will be very close to your research question from the existing literature which has been published within 5 years of time period.
Example:
As per previous published literature, a study was done by Singh HV et al. (2021) [13] on “Prevalence of diabetic retinopathy in self-reported diabetics among various ethnic groups and associated risk factors in North-East India: A hospital-based study” determined the prevalence of retinopathy was 44.93%, with 80% of statistical power, 95% confidence level and 10% allowable error, by using formula
n = Zα2 *p * q / d2
the calculated minimum sample size (N) = (4 * 44.93 * 55.07)/20.187 = 490.27 ~ 491 DM patients. But we want to take/round the total sample size as 500 DM patients to our present study.
Sample size calculation in case control Study
Case-control is a type of epidemiological observational study. It is often used to identify risk factors that may associated to a disease by comparing the risk factors in subjects who have that disease is called as “Cases” and with subjects who don’t have the particular disease which is called “Controls”.
Sample size calculation for unmatched case control studies needs the following assumptions like; the assumed number of cases and controls who experienced the risk factors from similar studies or from a pilot study and the researchers can use the assumed odds ratio, odds ratio, the level of confidence 95% and the proposed power of the study at least 80%. Using by some software/online software or reputed books that provide sample size to the researchers/investigators with the appropriate formula. But researchers should remember that, in the presence of a significant confounding factor, researchers required the minimum sample size. Since the confounding variables must be controlled for in any analysis, a more complex statistical model must be made, that’s why a larger sample is required to achieve significance.
Formula:
Sample Size =
(r + 1) (p*) (1 – p*) (Zβ + Zα/2)2
————————————-
r (p1 – p2)2
Here,
r = Ratio of control to cases, 1 for equal number of cases and controls
p* = Average proportion exposed = (proportion of exposed cases + proportion of Control exposed)/2
Zβ = Standard normal variate for power = for 80% power it is 0.84 ad for 90% value is 1.28. Researcher has to select power for the study.
Zα/2 = Standard normal variate for level of significance as mentioned in previous section
p1 – p2 = Effect size (or) different in proportion expected based on previous studies. p1 = proportion in cases ad p2 = proportion in Control.
Sample size formula-based on standard deviation
Sample Size =
(r + 1) (SD2) (Zβ + Zα/2)2
————————————-
r (d2)
SD = Standard Deviation = Researcher can take value from previously published studies
d = Expected mean difference between case ad control (the value based on previously existing literature/studies)
r – value from the previous studies.
Zβ = Standard normal variate for power = for 80% power it is 0.84 ad for 90% value is 1.28. Researcher has to select power for the study.
Zα/2 = Standard normal variate for level of significance as mentioned in previous section
Sample size calculation for Cohort Study:
Sample Size =
[ Zα √ (1 + 1/w) * (p*) (1 – p*) (Zβ * √ p1)
* (1 – p1)/m + p2 * (1 – p2)
————————————————————-
(p1 – p2)2
Here,
Zα = Standard normal variate for Level of Significance
w = Number of control subject per experimental subject
Zβ = Standard normal variate for power (or) Type 2 error as explained in earlier section
p1 = Probability of events in Control group
p2 = Probability of events in Experimental group
p*=
p2 + p1
———–
w + 1
Sample size calculation in Clinical Trials
Sample size is too small in clinical trials and it would well conducted study may fail to answer to the research hypothesis. Moreover, it may fail to find the important effects and relationship. Minimum information needed to calculate the sample size for a randomized controlled trial includes statistical power, level of significance, underlying event rate in the population and size of the treatment effect sought. Otherwise, calculated sample size should be adjusted for other factors including expected compliance rates and, less commonly, an unequal allocation ratio.
Based on some recommendations for different phases of clinical trials based on their sample size. In phase-I trial that involve drug safety on human participants/volunteers. Initial trials might require a total of around 20 to 80 patients. In phase-II trials that investigate the treatment effects, seldom require more than 100 to 200 patients.
Formula:
Sample Size =
(2SD2) (Zα/2 + Zβ)2
————————-
(d)2
Here,
SD = Standard Deviation = Researcher can take value from previously published studies
d = Effect Size = Difference between mean values (the value based on previously existing literature/studies, ie., Key Article)
r – value from the previous studies.
Zβ = Standard normal variate for power = for 80% power it is 0.84 ad for 90% value is 1.28. Researcher has to select power for the study.
Zα/2 = 1.96 (level of significance at 5%) from Z – table
Free software to calculate sample size and its links as shown in Table – 4.
Table – 4 Distribution of free software to calculate sample size and its links
Sample Size Calculation in Animal studies:
There are two methods of calculation of sample size in animal studies. The most preferred method is the same method which has been mentioned in sample size calculation for testing the hypothesis. So much of efforts is needed to calculate the sample size. It is not suitable for all the situation. At that time, sample size calculation by power analysis like standard deviation, effect size, and others. In that condition a second method can be used this is called as “resource equation method”. In this method the value ‘E’ is calculated based on decided sample size. If ‘E’ should within 10–20 then that is the correct sample size. If value of ‘E’ is <10 then more animal should be included and if it is >20 then sample size should be decreased.
The value of E = (Total no. of animals) – (Total no. of groups)
Suppose in an animal study a researcher formed 4 groups of animals having 8 animals each for different interventions then total animals,
= 32 (4 × 8). Hence, E value, E = 32 – 4 = 28
This is >20 hence animals should be decreased in each group. So, if researcher takes 5 rats in each group, then E value will be, E = 20 – 4 = 16. E is 16 which lies within 10-20 hence five rats per group for four groups. It will be considered as sample size (appropriately). This is a crude method and should be used only if sample size calculation can’t be done by power analysis method explained in above.
Conclusion
From this article, I have concluded that a researcher has to write the proposal for his/her studies, find the appropriate parent/key article, finding the risk factors related to your studies, and the final step is to find the sample size with the help of a statistical expert. Then only proceed the study by the researchers.
Limitations in the calculating sample size are as follows:
- Sample size calculated using the above formula is based on some modifications in Type-I and Type-II errors and few assumptions in effect size and standard variation.
- Enough/adequate and representative sample size always has to be calculated before initiating any study/research/survey and as far as possible should not be changed during the study course.
- Sample size calculation is also then influenced by a few practical issues. e.g., administrative issues and costs.
Source of funding: None
Conflict of Interest: Nothing to declared by the authors
Authors’ Contributions: SV – Authors contributed to the conceptualization, writing of the article and in preparation and checking of the article.
Here, SV – Senthilvel Vasudevan
References
- Hickey GL, Grant SW, Dunning J, Siepe M. Statistical primer: sample size and power calculations—why, when and how?, European Journal of Cardio-Thoracic Surgery 2018;54(1):4–9. DOI: https://doi.org/10.1093/ejcts/ezy169
- Patino CM, Ferreira JC. Inclusion and exclusion criteria in research studies: definitions and why they matter. J Bras Pneumol 2018;44(2):84. DOI: https://doi.org/10.1590/s1806-37562018000000088 PMID: 29791550; PMCID:
- Faber J, Fonseca LM. How sample size influences research outcomes. Dental Press J Orthod 2014;19(4):27-9. DOI: https://doi.org/10.1590/2176-9451.19.4.027-029.ebo PMID: 25279518; PMCID:
- National Sampling Survey: Ministry of Statistics and Programme Implementation, Government of India. Available from: https://www.mospi.gov.in/national-sample-survey-officensso [Accessed on: 11th July 2024]
- Das S, Mitra K, Mandal M. Sample size calculation: Basic principles. Indian J Anaesth 2016;60(9):652-656. DOI: https://doi.org/10.4103/0019-5049.190621 PMID: 27729692; PMCID:
- Kadam P, Bhalerao S. Sample size calculation. Int J Ayurveda Res. 2010;1(1):55-7. DOI:4103/0974-7788.59946. PMID: 20532100; PMCID: PMC2876926.
- OpenEpi: Open-Source Epidemiologic Statistics for Public Health. Available from: https://www.openepi.com/Menu/OE_Menu.htm [Accessed on: 13th July 2024]
- Epi Ifo: US Centres for Disease Control ad Prevention. Available from: https://www.cdc.gov/epiinfo/index.html [Accessed on: 13th July 2024]
- nMaster 2.0 Available from: https://nmaster.software.informer.com/2.0/ [Accessed on: 13th July 2024]
- Mohar D, Dulbarg CS. Statistical power, sample size, and their reporting in randomized controlled trials. JAMA. 1994;272:122–4. PMID: 8015121
- Thomas L, Juanes F. The importance of statistical power analysis: An example from animal behavior. Anim Behav 1996;52:856–9. [Google Scholar]
- Serdar CC, Cihan M, Yücel D, Serdar MA. Sample size, power and effect size revisited: simplified and practical approaches in pre-clinical, clinical and laboratory studies. Biochem Med (Zagreb) 2021;31(1):010502. DOI: https://doi.org/10.11613/BM.2021.010502 PMID: 33380887; PMCID:
- Singh HV, Shubhra D, Dipali D, Kalita IvaR. Prevalence of diabetic retinopathy in self-reported diabetics among various ethnic groups and associated risk factors in North-East India: A hospital-based study. Indian Journal of Ophthalmology 2021;69(11):3132-3137. DOI: https://doi.org/10.4103/ijo.IJO_1144_21
- Gaskill BN, Garner JP. Power to the People: Power, Negative Results and Sample Size. J Am Assoc Lab Anim Sci 2020;59(1):9-16. DOI: https://doi.org/10.30802/AALAS-JAALAS-19-000042 PMID: 31852563; PMCID:
![]() This is an open access journal, and articles are distributed under the terms of the Creative Commons Attribution‑Non-Commercial‑ShareAlike 4.0 International License, which allows others to remix, tweak, and build upon the work non‑commercially, as long as appropriate credit is given, and the new creations are licensed under the identical terms.
This is an open access journal, and articles are distributed under the terms of the Creative Commons Attribution‑Non-Commercial‑ShareAlike 4.0 International License, which allows others to remix, tweak, and build upon the work non‑commercially, as long as appropriate credit is given, and the new creations are licensed under the identical terms.
