Article Type: Editorial
Title: Statistical Significance, Effect Size and Confidence Intervals
Year: 2022; Volume: 2; Issue: 4; Page No: 3–4
Author: Karuthan Chinna 
https://doi.org/10.55349/ijmsnr.20222434
Affiliation: Professor, Faculty of Business and Management, UCSI University, Malaysia. Email ID: karuthan@ucsiuniversity.edu.my Phone No: +60 12 3758255
Article Summary: Submitted: 26-October-2022; Revised: 14-November-2022; Accepted: 02-December-2022; Published: 31-December-2022
Full Text
Introduction
Over the years, statistical significance has been the cornerstone of inferential statistics. In testing a treatment effect, the null hypothesis is often written as ‘no effect’ and the alternative is written as ‘there is an effect’. The significance test yields a p-value that is usually compared with the conventional value of 0.05. If the p-value is less than 0.05, the null hypothesis is rejected, and a statistical significance is said to be established. Obtaining significant results is a tremendous accomplishment but it does not tell the entire story behind the results.
For example, if we want to test if a new drug is effective in the management of hypertension. We would state the null hypothesis as ‘there is no change’ (mean difference = 0) and the alternative hypothesis as ‘there is a change’ (mean difference ≠ 0). In a single-armed study, we would select a few patients (n) with hypertension, record their baseline blood pressure (BP) values, administer the drug, for about two weeks, and measure their BP again after two weeks. To assess the efficacy of the drug, usually the paired samples t-test would be used [1]. In this test, the pairwise differences in the individual patient’s BP are computed and the mean difference is compared against the value of 0. In this test, based on the absolute mean difference(M), standard deviation(S) and sample size(n), a t-statistics is computed as:
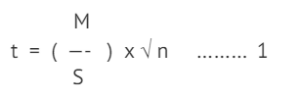
In (1), t is a continuous value that stretches from negative to positive and is said to follow a t-distribution. The curve is symmetrical and ‘bell-shaped’, peaking at 0 and tapering off to the right and left of 0. When there is no change at all, M will be 0 and t will be 0 too. The area under the curve, that is the p-value, to the right of t=0 will be 0.5 (half the area under the curve). Conventionally, when the p-value is < 0.05, the following is inferred: t is large, M is far from 0, and hence there a significant change in BP. If the change is in the desirable direction, the drug is said to be effective. For practical purposes, when t is >2, the p-value is taken as less than 0.05.
Example: 1
M = 5.0, S = 10.0, n = 25;
the p-value will be < 0.05
In example (1), note that even when M is small in absolute value, for a large n, t will be far from 0 and the p-value will be less 0.05, making us make the same conclusion; there is a significant change in mean BP.
Example: 2
M = 1.1, S = 10.0, n = 400;
But, the question is, is a mean reduction of 1.1 mmHg of any clinical importance? This makes us ponder on the usage of the evidence presented in the form of p-values alone. It appears we can prove anything is ‘significant’ as long as we have an adequate sample size.
In equation (1), the term
is called the effect size (ES). Note that it is not amplified
by the sample size. That is, ES is the real difference, irrespective of sample size. Effect size is typically expressed as Cohen’s d. Cohen described a small effect = 0.2, medium effect size = 0.5 and large effect size = 0.8 [2]. In example (1), ES = 5/10 = 0.5, which is moderate and in example (2), ES = 1.1/10 = 0.11, which is very small. But based on p-value alone, both are statistically significant results. This highlights an important point: do not assess evidence from the statistical point alone, look at practical evidence as well. In 2014, The Basic and Applied Social Psychology editorial emphasized that the null significance testing procedure should be discouraged. [3]
Other researchers recommend reporting confidence intervals (CI), incorporating accuracy (or margin of error, ME) as M ± ME [4]. For practical purposes, ME for testing means is,
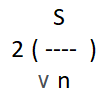
where, 2 is the approximate constant value for a 95% CI. For example, a 95% CI for mean difference of [5, 8], would be interpreted as ‘we are 95% confident the mean difference will be between 5 and 8’.
In example (1),
Hence, the 95% is 5.0±2 = [3.0, 7.0]
In example (2), ME =
Hence, the 95% is 1.1±1 = [0.1, 2.0]
In example (2), ME is half of that in example (1), and hence the interval is much narrower (more precise), which is good. However, looking at the evidence, in example (2), the lower limit of 0.1, hardly misses the value of 0, indicating the possibility of there being no change.
Results for example (1) would be reported as ‘the mean difference is 5.0 (95% CI = 3.0, 7.0, p<0.05). Stating the CI as well gives a better indication of the drug effect. In this case, the drug is effective.
Results for example (2) would be reported as ‘the mean difference is 1.1(95% CI = 0.1, 2.0, p<0.05). It is clear the p-value is inflated by the huge sample size (statistical evidence), but the effect is low (clinical evidence).
According to Cumming, researchers should always report confidence intervals, as it conveys what a p-value does not: the magnitude and relative importance of an effect [4]
References
- Chinna K, Krishnan K. Biostatistics for the Health Sciences. 2009; Publisher McGrawHill Malaysia. ISBN-13: 978-983385686
- Cohen J. Statistical Power Analysis for the Behavioral Sciences (2nd). 1998;Hillsdale, New York:Lawrence Erlbaum Associates, Publishers. ISBN: 0-8058-0283-5. Available from: https://www.utstat.toronto.edu/~brunner/oldclass/378f16/readings/CohenPower.pdf
- Nuzzo R. Scientific method: Statistical errors. Nature 2014;506:150–152. DOI: https://doi.org/10.1038/506150a
- Cumming G. Understanding the New Statistics: Effect sizes, Confidence Intervals, and Meta-Analysis. Routledge: New York 2012;1-536. ISBN:
This is an open access journal, and articles are distributed under the terms of the Creative Commons Attribution‑Non-Commercial‑ShareAlike 4.0 International License, which allows others to remix, tweak, and build upon the work non‑commercially, as long as appropriate credit is given, and the new creations are licensed under the identical terms.
